KTUGFaqKTUG FAQ
![[http]](/wiki/imgs/http.png)
You will overcome the attacks of jealous associates.
FrontPage › SymPy
SymPy는 Mathematic나 Maple에서 하듯이 심볼 계산을 지원하는 Python 모듈이다.
이 모듈의 Printing 기능을 이용하면 [편집]
Python 예제: latexdemo.py ¶
from sympy import * from sympy.abc import x print( latex(x**2) ) print( latex(1/x) ) print( latex(Integral(x**2, x)) ) print( latex(integrate(x**2, x)) ) print( latex((1/cos(x)).series(x, 0, 6)) )
실행 결과:
${x}^{2}$
$\frac{1}{x}$
$\int {x}^{2}\,dx$
$\frac{1}{3} {x}^{3}$
$1 + \frac{1}{2} {x}^{2} + \frac{5}{24} {x}^{4} + \operatorname{\mathcal{O}}\left({x}^{6}\right)$
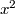
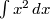
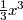
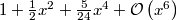
이 것 참 재미 있네요. 좋은 정보 감사합니다.
