[편집]
2 짧은 명령어 만들지 말고 구이(GUI)로 입력하자 ¶
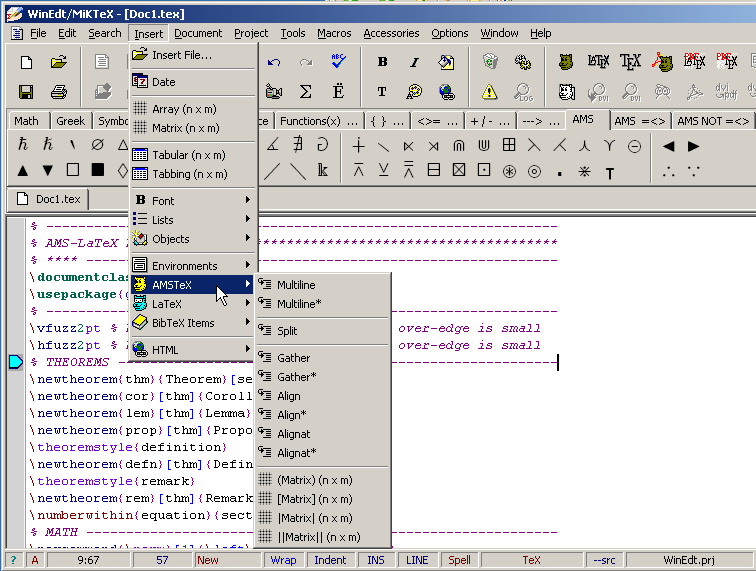
그림 1: WinEdt는 LaTeX과 AMSLaTeX의 수식 환경의 뽄(型板: Template)를 많이 구비하고 이들을 구이(GUI)로서 쉽게 불러 오도록 만들어 두었다.->  837참조, TeX 문서의 뽄(Template) 입력 방법은 WinEdtTip/Templates의 항목 "새 문서의 뽄" 참조
837참조, TeX 문서의 뽄(Template) 입력 방법은 WinEdtTip/Templates의 항목 "새 문서의 뽄" 참조
TeX 문서에 수식 모드(디스플레이 형이든 본문 형이든)를 만들 때는 먼저 수식의 내용(Text)을 입력하고 그 내용을 선택한 다음(선택한 내용은 파랑 바탕에 흰 글씨로 변함) 위의 그림에서 처럼 메뉴에서 Insert를 누르고 메뉴판과 보조메뉴판이 나타나면 원하는 환경을 선택하는 것이 편하다. 학술회의의 프로시딩이나 학술지에 투고한 글 중에는 간혹
\newcommand{\bdm}{\begin{displaymath}}
\newcommand{\edm}{\end{displaymath}}
\newcommand{\beq}{\begin{equation*}\begin{split}}
\newcommand{\eeq}{\end{equation*}}
처럼 디스플레이 형 수식 명령어를 새로 정의하여 쓰는 경우를 볼 수 있는 데 이렇게 하면 "delimiter 짝찾기" 기능(WinEdtTip/Delimiters관리)이 듣지 않는다. 그래서 오류가 생겼을 때 오류를 찾아가기가 힘들 때도 있다. 어떤 때는 오류 메시지 다음에서 Enter를 치면 바로 소스 파일의 마지막 \end{document}로 가는 수도 있다. 특히 위의 예와 같이 수식 환경의 명령어를 새로 정의한 경우 \beq ... \end{split}\eeq로 쓰는 것을 깜박 잊고 \beq ... \eeq만 쓰면 split 환경 속에 들어갔다가 나오지 않았는데 equation* 환경을 닫았버렸기 때문에
Runaway argument?
\plus _{x\in X} \eeq
! Paragraph ended before \split was complete.
<to be read again>
\par
l.15
와 같이 오류 메시지가 나타나면서 더 이상 컴파일하지 못하는 경우가 있다.
한편 수식 환경을 만든 후 한 행을 띄울 것인가 아닌가는 다음을 새 문단으로 할 것인가 아닌가에 따라 결정한다. 구태여 \indent 또는 \noindent 등의 명령어를 쓸 필요는 없다.
$...$, \(...\), $$...$$, \[...\]등으로 입력되어 있는 수식 모드를 equation 환경 (또는 equation* 환경)[1]으로 바꾸거나 한 행으로 된 수식이 너무 길어서 split 환경이나 aligned 환경을 넣어 두 행 또는 세 행으로 나눈다거나, LaTeX의 환경인 eqnarray 환경(또는 eqnarray* 환경)을 AMS-LaTeX의 환경인 align 환경 (또는 align* 환경, alignat 환경, alignat* 환경, flalign 환경, flalign* 환경)으로 수작업으로 바꾸는 것은 매우 신경쓰이는 일이다. 이 것을 WinEdt의 구이(GUI) 단추를 이용하면 쉽게 바꿀 수 있다. 몇가지 요령이 필요하다.
[편집]
2.1 $$...$$ 등을 equation* 환경으로 바꾸기 ¶
수식 번호가 필요없는 수식이라도 $$...$$, \[...\] 등으로 입력하는 것 보다는 begin{equation*}... \end{equation*}로 입력하는 것이 훨씬 좋다. 수식에 Tag를 달기도 편하고, 한 행의 수식을 여러 행으로 나눌 때도 편하다. 또 증명이 끝났다는 표시로 쓰이는 정사각형 Box도 명령어 \qedhere로 쉽게 해결할 수 있다. 가령
Now, define a relation $ \eta_1 $ as:
\begin{center}
$ \eta_1=\sigma \cap \rho_1. $
\end{center}
로 된 것을 수식 환경으로 바꾸려면 "\begin{center} $" 와 "$ \end{center}"를 지워버리면
Now, define a relation $ \eta_1 $ as: \eta_1=\sigma \cap \rho_1.로 변한다. 여기서 "\eta_1=\sigma \cap \rho_1."만 선택(선택된 부분은 파랑 바탕이 됨)하고 메뉴에서 Insert -> Environments -> Equation* 를 찾아가서 클릭하면
Now, define a relation $ \eta_1 $ as:
\begin{equation*}
\eta_1=\sigma \cap \rho_1.
\end{equation*}
로 변한다. 만약 수식 끝에
\tag{since $S$ is quasi-inversive}
를 달면 수식의 왼쪽 가장자리(AMS의 클래스에서 옵션 없이, article 클래스에서는 leqno 옵션을 썼을 때) 또는 오른쪽 가장자리(article 클래스에서 옵션 없이, AMS의 클래스에서는 reqno 옵션을 썼을 때)에
(since S is quasi-inversive)
로 나타난다.
[편집]
3.1 수식 번호를 왼쪽/오른쪽에 ¶
클래스 옵션이 leqno이면 번호는 수식의 왼쪽 가장자리에, reqno이면 번호는 수식의 오른쪽 가장자리에 붙는다. AMS의 클래스에서 옵션을 안썼을 때는 leqno이고, article 클래스에서 옵션을 안썼을 때는 reqno이다.
[편집]
5.1 묶음표와 정렬(Alignment) ¶
\left 와 \right 가 들어가는(위치를 나타내는) 묶음표는 같은 수식 표현 속에서 완성하여야 한다. 즉, \left 와 \right 사이에는 줄바꿈(\\) 또는 탭(&) 등이 들어가면 오류메시지가 나타난다. 따라서 묶음표가 여러 수식 표현에 갈라져 나타날 때는 크기 명령어(\Bigg, \bigg, \Big, \big 등)가 위치 명령어(\left, \right)보다 편하다. 위치 명령어는 반드시 왼쪽과 오른쪽이 있어야 오류 메시지가 나타나지 않는다. 즉 어느 한 쪽 묶음표가 필요 없을 때는 \left., \right.를 써야 한다. ->  982,
982,  19587
19587
[편집]
5.2 한 수식이 너무 길 때 ¶
split: AMS-LaTeX에서는 equation 환경(또는 equation* 환경)에서 수식을 입력하다가 여러 행이 필요하면 eqnarray 환경으로 바꿀 필요 없이 equation 환경 내에서 수식 text만을 split 환경이나 aligned 환경으로 감싸면 된다. 이 때 수식 번호는 (옵션을 택하지 않았을 때) 하나만 상하 가운데 붙는다. 옵션에 대해서는 amsldoc.pdf의 2쪽에 있다.
\begin{equation}\label{eq01}
\begin{split}
g(A) & = g_1(A) + g_2(A) \\[5pt]%다음 줄과의 간격 5pt를 더할 때
& = \sum_{i=1}^2 g_i(A)
\end{split}
\end{equation}
와 같이하면 해결된다.
multline: 한 수식을 여러 행으로 나누어 쓰는 방법에는 multline(multiline이 아니고 multline, 아이(i)를 조심) 환경도 있다. multline 환경에서는 첫 행은 왼쪽 정렬이고 끝 행은 오른쪽 정렬, 가운데 행들은 모두 가운데 정렬이 된다. 가운데 행을 왼쪽 정렬로 하고 싶으면 \shoveleft{내용}\\ 로 입력, 오른쪽 정렬로 하고 싶으면 \shoveright{내용}\\ 로 입력한다. 또 가운데 행을 약간 왼쪽 또는 오른쪽으로 옮기려면 \hskip-10pt 또는 \hskip10pt (수치는 조정 가능)을 행의 앞에 넣으면 된다.
multline 환경에서는 여러 행에 걸친 수식이라도 하나의 수식으로 보고 번호가 하나만 붙는다.클래스 옵션이 leqno 이면 수식 번호는 첫 행의 앞에, reqno 이면 수식 번호는 끝 행의 뒤에 붙는다. 수식 번호가 필요 없으면 multline* 환경을 쓰면 된다.
[편집]
5.3 여러 행에 수식 번호 하나를 ¶
aligned: 이미 여러 행 수식이 만들어져 있고, 각 행이 각각의 수식 번호를 갖도록 되어 있을 때 전체를 하나의 수식으로 보고 하나의 번호를 부여하고 싶을 때는 원래의 환경을 aligned 환경으로 바꾼 후 aligned 환경 전체를 다시 equation 환경으로 감싸면 된다. 이때 GUI 단추를 이용하면 편리하다.
Q: (From  16290)
16290)
\begin{equation}
\begin{split}
x&=a+b \qquad if\ x>0 \\
x&=c \qquad otherwise \\
\end{split}
\end{equation}
로 하면
x=a+b if x<0 x=c otherwise로 나옵니다. \quad \: 같은 스페이스를 넣지 않고 if 와 otherwise를 정렬 시키려면 어떻게 해야 하나요? 한줄에 &를 두개 쓰면 컴파일할 때
!Extra alignment tab has been changed to \cr라는 에러가 납니다.
A: split 환경에서는 탭 &을 각 행에 한 번 밖에 못 씁니다. equation 환경 안에 쓸 수 있는 것으로 aligned 환경이 좋을 것 같습니다. aligned 환경 안에서는 &의 숫자가 일정하지 않아도 되고 &을 여러 번 넣게 되면 각 열의 정렬은
rl rl ...식으로 rl을 되풀이 합니다. 즉 홀수 열은 오른쪽 정렬, 짝수 열은 왼쪽 정렬이 됩니다. 만약 맨 첫 열을 왼쪽 정렬에서 시작하려면 각 행의 앞에 &을 넣으면 됩니다. 다음을 컴파일하여 보세요.
\documentclass{amsart}
\begin{document}
\begin{equation}
\begin{aligned}
&x=a+b &&\textrm{if}\quad x<0 \\
&x=c &&\textrm{otherwise}
\end{aligned}
\end{equation}
\end{document}
[편집]
5.4 Eqnarray 환경을 Align 환경으로 바꾸기 ¶
여러 행의 수식을 나열할 때 LaTeX에서는 보통 eqnarray 환경(또는 eqnarray* 환경)을 쓰는 데 eqnarray에서는 세 열까지만 쓸 수 있고 열의 정렬이 rcl로 되어 있어 탭 &을 두 번까지만 쓸 수 있다. 그래서 각 행에 =이 한 번씩 들어갈 때 즉,
A&=&B &=&C등으로 나열되는 수식에 많이 쓴다. 그리고 각 열 사이의 간격(탭 &이 들어간곳)은 다른 수식 환경에서 보다 많이 벌어진다. 그래서 수식을 왼쪽 정렬하려면 각 행의 머리에 두 번의 탭 &&을 넣어야 한다. 또 일단 두 번의 탭 &&을 모두 썼으면 그 다음은 수작업으로 정렬시킬 수 밖에 없다. 이에 반해서 AMS-LaTeX에는 align 환경, alignat 환경, flalign 환경 (또는 align* 환경, alignat* 환경, flalign* 환경) 등 다양한 환경을 갖고 있고 각 행에 쓸 수 있는 탭 &의 숫자도 제한이 없다. &을 여러 번 넣게 되면 각 열의 정렬은
rl rl ...식으로 rl을 되풀이 된다. 즉 홀수 열은 오른쪽 정렬, 짝수 열은 왼쪽 정렬이 된다. 만약 맨 첫 열을 왼쪽 정렬에서 시작하려면 각 행의 앞에 탭 &을 하나 더 넣으면 된다. 또 eqnarray 환경(또는 eqnarray* 환경)은 수식 행의 끝에 \tag{설명}을 넣을 수 없지만 align 환경 (또는 align* 환경)은 각 행에 \tag{설명}으로 (설명)을 붙일 수 있다. \tag은 클래스 옵션에 따라 (수식 번호와 함께) 왼쪽 끝 또는 오른쪽 끝에 붙는다.
[편집]
5.7 여러 행 수식을 활짱묶음표(Brace)로 묶기 ¶

소스:
\documentclass{article} \usepackage{amsmath} \usepackage{cases} \begin{document} \begin{equation}\label{} P_{r-j}=\begin{cases} 0& \text{if $r-j$ is odd},\\ r!\,(-1)^{(r-j)/2}& \text{if $r-j$ is even}. \end{cases} \end{equation} \begin{numcases}{X =} 1 & explanation 1 \\ 2 & explanation 2 \\ ... \\ n & explanation n \end{numcases} \begin{subnumcases}{X =} \begin{aligned} \phi_{\mathcal{PI}} &= \sum_{i=1}^N \phi_i \\ % &= \sum_{i=1}^N \Big[c_bu_i + f_b {1}_{\{u_i\neq0\}}\Big] \end{aligned}\\ \begin{aligned} \phi_{\mathcal{PF}} &= \sum_{i=1}^N \Big[c_su_i(1+r_i) + f_s {1}_{\{u_i(1+r_i)\neq0\}}\Big] \end{aligned} \end{subnumcases} \end{document}
[편집]
6.1 단위 행렬 ¶

그림 설명: ![[http]](http://faq.ktug.org/wiki/imgs/http.png) Math mode - v.2.21(http://ftp.ktug.or.kr/tex-archive/info/math/voss/mathmode/Mathmode.pdf)의 60.1절
Math mode - v.2.21(http://ftp.ktug.or.kr/tex-archive/info/math/voss/mathmode/Mathmode.pdf)의 60.1절
![[http]](http://faq.ktug.org/wiki/imgs/http.png) Math mode - v.2.21(http://ftp.ktug.or.kr/tex-archive/info/math/voss/mathmode/Mathmode.pdf)의 60.1절
Math mode - v.2.21(http://ftp.ktug.or.kr/tex-archive/info/math/voss/mathmode/Mathmode.pdf)의 60.1절
[편집]
6.2 파티션된 행렬 ¶
행렬을 나타내기 위하여 꼭 matrix 환경을 쓰는 것은 아니다.
예1: 가령

를 나타내기 위하여
 /info/examples/tlc2/에 있는 5-6-4.ltx 와 5-6-5.ltx 를 참고하여 만들었다. 수식 모드 내에 tabular 환경을 썼는 데 tabular 환경 내는 수식 모드가 아니기 때문에 수식을 쓸려면 다시 수식 모드로 만들어야 한다.
/info/examples/tlc2/에 있는 5-6-4.ltx 와 5-6-5.ltx 를 참고하여 만들었다. 수식 모드 내에 tabular 환경을 썼는 데 tabular 환경 내는 수식 모드가 아니기 때문에 수식을 쓸려면 다시 수식 모드로 만들어야 한다.
\documentclass{article}%
\usepackage{array,arydshln}%For dashed rules
\begin{document}
\setlength\extrarowheight{2pt}%extra space on row top
\renewcommand\arraystretch{1.15}%extra space evenly distributed
\setlength\dashlinedash{2pt} \setlength\dashlinegap{2pt}
$$
\left[\begin{tabular}{cc:c}
$A$ & $B$ & $C$ \\
$X$ & $Y$ & $Z$ \\ \hdashline
100 & 10 & 1 \\
\end{tabular}\right]
$$
\end{document}
와 같이 입력하는 수도 있다. 참고: 이 소스 코드는 예2: 또

를 나타내기 위하여
\documentclass{article}
\usepackage{amsmath}
\usepackage{hfont}
\newcommand{\je}{\text{제}}
\newcommand{\yl}{\text{열}}
\def\cntclmn#1{\multicolumn{1}{c}{#1}}
\begin{document}
\begin{tabular}{|ccc|}
\cntclmn{\je} & \cntclmn{\je} & \cntclmn{\je} \\[-4pt]
\cntclmn{1} & \cntclmn{2} & \cntclmn{3} \\[-5pt]
\cntclmn{\yl} & \cntclmn{\yl} & \cntclmn{\yl} \\[2pt]
$a$&$b$&$c$\\
$d$&$e$&$f$\\
$g$&$h$&$i$
\end{tabular}
\end{document}
와 같이 입력하는 수도 있다. 참고: 역시 tabular 환경 내는 수식 모드가 아니기 때문에 수식을 쓸려면 수식 모드로 만들어야 한다. 행렬식의 간격이 고르지 않아 수학하는 사람들의 마음에는 들지 않을 수도 있다.
[편집]
6.3 smallmatrix, 복호(復號) ¶
Q1(from  15746): 수식에서 행렬을 쓰고 싶을 때는, begin{displaymath} 를 쓰는 방법만 알고 있습니다.
그렇게 하면, 문장이 이어지는 것이 아니라, 행렬만 따로 떨어져서 나오게 되네요. 예를 들어,
15746): 수식에서 행렬을 쓰고 싶을 때는, begin{displaymath} 를 쓰는 방법만 알고 있습니다.
그렇게 하면, 문장이 이어지는 것이 아니라, 행렬만 따로 떨어져서 나오게 되네요. 예를 들어,
Since x=|1 2|, det x is not zero.
|3 4|
이런 문장을 쓰고 싶은데, display math를 쓰면, 이것이 문장으로 연결되지 않고, 행렬만 떨어져 따로 display 되네요. 문장 전체를 displaymath하면 되기는 하지만, 그렇게 하고 싶지는 않고요. 방법을 알았으면 좋겠습니다.
A(from  115748): (커꿈) amsmath 패키지의 smallmatrix 환경을 사용하시면 됩니다.
115748): (커꿈) amsmath 패키지의 smallmatrix 환경을 사용하시면 됩니다.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
The matrix
$\left(
\begin{smallmatrix}
1 & 0 \\
0 & 1
\end{smallmatrix}
\right)$
is called the identity matrix.
\end{document}
Q2(from  18208): \rightarrow와 \nrightarrow를 아래위로 나란히 나오게 하고 싶습니다.
18208): \rightarrow와 \nrightarrow를 아래위로 나란히 나오게 하고 싶습니다.
\rightrightarrow와 비슷한데, 아래쪽 화살표를 \rightarrow 대신 \nrightarrow로 바꾼 셈입니다.
\atop 같은 걸로 \rightarrow와 \nrightarrow를 쌓아 보니, 두 기호 사이의 간격이 너무 벌어집니다.
어떻게 하면 될까요?
A(from  18210): 다음을 컴파일하면 아래 그림과 같이 나옵니다.
18210): 다음을 컴파일하면 아래 그림과 같이 나옵니다.
\documentclass{article}
\usepackage{amsmath,amssymb}
\begin{document}
$A \begin{smallmatrix}
\rightarrow \\[-2pt]
\nrightarrow
\end{smallmatrix} B$\qquad
$A \begin{smallmatrix}
\rightarrow \\[-2pt]
\nleftarrow
\end{smallmatrix} B$\qquad
$A \begin{smallmatrix}
\leftarrow \\[-2pt]
\nrightarrow
\end{smallmatrix} B$
\end{document}
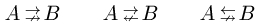
[편집]
6.4 분수 표시, 조합 표시, 2 X 1 행렬 ¶
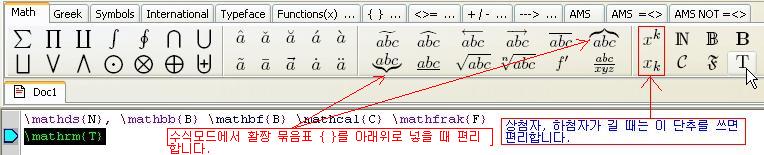
그림 3: WinEdt의 기호 GUI 페이지들 중 Math 견출(탭)를 선택하면 "xyz 분의 abc"로 표시된 단추가 있다. 이 단추를 누르면 \frac{}{}이 입력된다. \frac{분자}{분모}로 입력하면 된다. 이것은 주위의 모드에 따라 크기가 변한다. 가령 "m분의 n"을 나타내는 데 $\frac{n}{m}$이면 본문 형, $$\frac{n}{m}$$이면 디스플레이 형이 된다. 굳이 디스플레이 형, 본문 형을 지정하려면 \dfrac{n}{m}, \tfrac{n}{m} 등으로 입력하면 된다.
한 편 n 개에서 m 개를 선택하는 "경우의 수"(조합)를 나타내는 손톱묶음 () (2 X 1 행렬)은 $\binom{n}{m}$, $$\binom{n}{m}$$, $\dbinom{n}{m}$, $$\tbinom{n}{m}$$ 등으로 입력한다. 이것의 응용으로 본문 속에 2 X 3 행렬 $\binom{1\;2\;3}{0\;0\;0}$을 줄(행) 간격을 늘리지 않고 넣을 수 있다.
참고: 여기서 사용하는 명령어 \frac{}{}, \dfrac{}{}, \tfrac{}{}, \binom{}{}, \dbinom{}{}, \tbinom{}{}는 모두
\genfrac{왼쪽 묶음표}{오른쪽 묶음표}{가로 선의 굵기}{스타일}{분자}{분모}
로 정의되는 명령어 \genfrac의 특별한 경우로 {분자}{분모}만 선택하여 넣으면 되도록 만들어져 있다. 그리고 네째 묶음표{} 속에는 0, 1, 2, 3의 숫자를 넣을 수 있는데 0은 '디스플레이 형', 1은 '본문 형'(\textstyle), 2는 \scriptstyle, 3은 \scriptscriptstyle 이다. 비워 두면 모드이의 응용으로 가령 2 X 1 행렬을 꺾쇠 묶음표 []로 하고 싶으면
\newcommand\tbmatrix[2]{\genfrac{[}{]}{0pt}{}{#1}{#2}}
로 프리앰블에 정의하여 두고 필요한 곳에서 $\tbmatrix{n}{m}$과 같이 쓸 수 있다. 이것의 응용으로 본분 속에 2 X 3 행렬 $\tbmatrix{1\;2\;3}{0\;0\;0}$을 줄(행) 간격을 늘리지 않고 넣을 수 있다.
[편집]
7 외부 프로그램 이용하기 ¶
TeXaide:
http://www.winedt.org/Plugins/ 에 가면 WinEdt와 함께 쓸 수 있는 프로그램들이 있다. TeXaide는 WysiWyg으로 편집한 수식을 TeX의 수식 모드에서 쓸 수 있는 코드로 바꿔 준다. ![[http]](http://faq.ktug.org/wiki/imgs/http.png) TeXaide(http://www.dessci.com/features/taform.stm) 참조
TeXaide(http://www.dessci.com/features/taform.stm) 참조
![[http]](http://faq.ktug.org/wiki/imgs/http.png) TeXaide(http://www.dessci.com/features/taform.stm) 참조
TeXaide(http://www.dessci.com/features/taform.stm) 참조
EqMagicLite:
"Equation Magic"(See EqMagicLite)도 같은 기능을 한다.
죄송: 시간이 없어 미완성인 채로 남겨 둡니다. 시간이 나는 데로 고쳐 가겠습니다.-Yhchoe